0x01 陷门函数
trapdoor function是一种重要的函数。也是现代密码学依赖的几种特殊函数之一。trapdoor function与哈希函数有些类似,即正向容易求解,反向很难或者不可能求解(除非知道原始信息)。即,如果没有人有密钥或钥匙,他们不能反转功能。
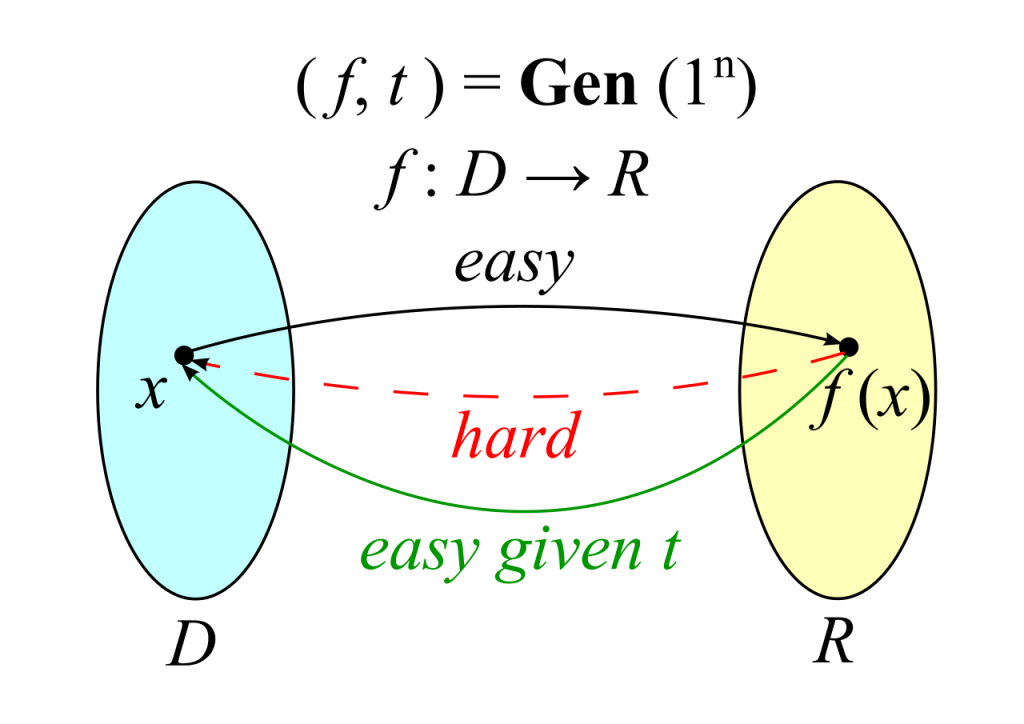
trapdoor function:陷门函数。数学术语来说,如果f是活板门函数,则存在一些秘密信息t,使得给定f(x)和t,就很容易计算x。考虑一个挂锁及其钥匙。通过将钩环推入锁定机构,无需使用钥匙即可将挂锁从打开状态更改为关闭状态,这很简单。但是,轻松打开挂锁需要使用钥匙。这里的钥匙是活板门,挂锁是活板门功能。 trapdoor function构成了现代密码技术的基础,这些技术在网上被广泛使用。
0x02 公钥密码学
密码学的历史可以分为两个时代:古典时代和现代时代。两者的转折点发生在 1977 年,当时同时引入了RSA 算法和Diffie-Hellman密钥交换算法。这些新算法是革命性的,因为它们代表了第一个可行的密码方案,其中安全性基于数论。它是第一个在没有共享秘密的情况下实现两方之间安全通信的技术。密码学从关于在世界各地安全地传输秘密密码本发展到能够在任何两方之间进行可证明的安全通信,而无需担心有人在窃听密钥交换。
现代密码学是建立在这样一种思想之上的,即您用于加密数据的密钥可以公开,而用于解密数据的密钥可以保密。因此,这些系统被称为公钥密码系统。第一个,也是最广泛使用的系统,被称为 RSA——以首次公开描述该算法的三个人的首字母命名:Ron Rivest、Adi Shamir 和 Leonard Adleman。
要使公钥密码系统正常工作,您需要一组算法,这些算法易于单向处理,但难以撤消。在 RSA 的情况下,简单算法将两个素数相乘。如果乘法是简单的算法,那么它的困难配对算法是将乘法的乘积分解为其两个分量素数。具有这一特征的算法——一个方向容易,另一个方向难——被称为陷阱门函数。找到一个好的陷门函数对于制作安全的公钥密码系统至关重要。简单地说:在陷门函数中向一个方向前进的难度与向另一个方向前进的难度之间的差距越大,基于它的密码系统就越安全。
一般来说,公钥加密系统有两个组成部分,一个公钥和一个私钥。加密的工作原理是获取一条消息并对它应用数学运算以获得一个看起来随机的数字。解密采用随机数字并应用不同的操作来恢复原始数字。使用公钥加密只能通过使用私钥解密来撤销。
计算机不能很好地处理任意大的数字。我们可以通过选择最大数字并仅处理小于最大值的数字来确保我们正在处理的数字不会变得太大。我们可以将数字视为模拟时钟上的数字。任何导致数字大于最大值的计算都会被环绕到有效范围内的数字。
0x03 RSA 算法
RSA 算法是最流行和最容易理解的公钥密码系统。
在 RSA 中,这个最大值(称为max)是通过将两个随机素数相乘获得的。公钥和私钥是两个特别选择的大于零且小于最大值的数字,称为pub和priv。要加密一个数字,请将其乘以它本身的发布时间,确保在达到最大值时回绕。要解密消息,您将其乘以priv时间,然后返回原始数字。这听起来令人惊讶,但它确实有效。这一特性在被发现时是一个重大突破。
要创建 RSA 密钥对,首先随机选择两个素数以获得最大值(max)。然后选择一个数字作为公钥pub。只要知道这两个素数,就可以根据这个公钥计算出对应的私钥priv。这就是分解与破坏 RSA 的关系——将最大数量分解为其组成素数允许您从公钥计算某人的私钥并解密他们的私人消息。
让我们通过一个例子来更具体地说明这一点。以质数 13 和 7 为例,它们的乘积给出了我们的最大值 91。让我们把我们的公共加密密钥作为数字 5。然后利用我们知道 7 和 13 是 91 的因数这一事实,并应用一种称为扩展欧几里得算法,我们得到私钥是数字 29。
这些参数(最大值:91,pub:5;priv:29)定义了一个功能齐全的 RSA 系统。您可以取一个数字并将其自身相乘 5 次以对其进行加密,然后取该数字并将其自身相乘 29 次,即可得到原始数字。
让我们使用这些值来加密消息“CLOUD”。
为了在数学上表示消息,我们必须将字母转换为数字。拉丁字母的常见表示是 UTF-8。每个字符对应一个数字。
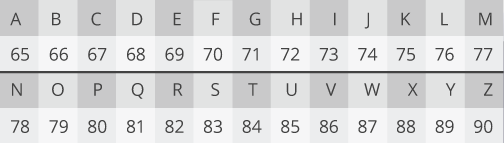
在这种编码下,CLOUD 是 67、76、79、85、68。这些数字中的每一个都小于我们最大的 91,因此我们可以单独加密它们。让我们从第一个字母开始。
我们必须将它自己乘以 5 次才能得到加密值。
67×67 = 4489 = 30 *
*由于 4489 大于最大值,我们必须将其环绕。我们通过除以 91 并取余数来做到这一点。
4489 = 91×41 + 30
30×67 = 2010 = 8
8×67 = 536 = 81
81×67 = 5427 = 58
这意味着 67 的加密版本是 58。
对我们得到的每个字母重复该过程,加密消息 CLOUD 变为:
58、20、53、50、87
为了解密这个加扰的消息,我们将每个数字乘以自身 29 次:
58×58 = 3364 = 88 (记住,当数字大于max时我们回绕)>
88×58 = 5104 = 8
…
9×58 = 522 = 67
瞧,我们回到了 67。这适用于其余数字,从而产生原始消息。
要点是,您可以取一个数字,将其与自身相乘多次以获得看起来随机的数字,然后将该数字与自身相乘一个秘密次数以返回原始数字。
0x04 不是完美的陷门
RSA 和 Diffie-Hellman 之所以如此强大,是因为它们带有严格的安全证明。作者证明,打破系统等同于解决一个被认为难以解决的数学问题。因式分解是一个众所周知的问题,自古以来就一直在研究(参见埃拉托色尼筛法)。
也就是说,保理并不是最难的问题。二次筛和通用数域筛等专门算法是为了解决素数分解问题而创建的,并且取得了一定的成功。与仅猜测已知素数对的天真方法相比,这些算法更快且计算量更少。
随着被分解的数字的大小变得越来越大,这些分解算法变得更加有效。随着数字(即密钥的位长度)变大,分解大数和乘以大数的难度之间的差距正在缩小。随着可用于解密数字的资源的增加,密钥的大小需要增长得更快。对于计算能力有限的移动和低功率设备来说,这不是一个可持续的情况。从长远来看,因式分解和乘法之间的差距是不可持续的。
所有这一切都意味着 RSA 不是密码学未来的理想系统。在理想的陷门函数中,相对于所讨论数字的大小,简单方法和困难方法以相同的速度变得更难。我们需要一个基于更好陷门的公钥系统。
0x05 椭圆曲线
椭圆曲线是满足特定数学方程的一组点。椭圆曲线的方程如下所示:
y^2 = x^3 + ax + b
该图形看起来有点像侧面倾斜的 Lululemon 徽标:
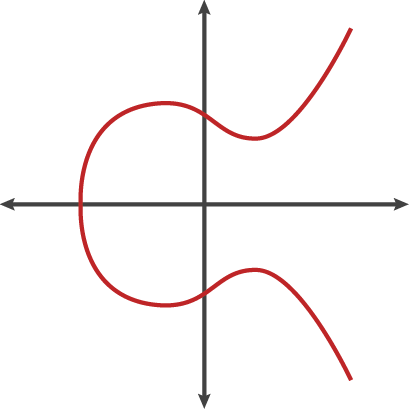
椭圆曲线还有其他表示,但从技术上讲,椭圆曲线是在两个变量中满足方程的设定点,其中一个变量的度数为 2,另一个变量的度数为 3。椭圆曲线不仅仅是一张漂亮的图片,它还具有一些特性,使其成为密码学的良好设置。
人们喜欢吹嘘加密货币“受数学保护”,但通常很少谈论所涉及的实际数学。椭圆曲线看起来像上面时髦的马蹄形,很容易计算为满足一个简单方程的点集:
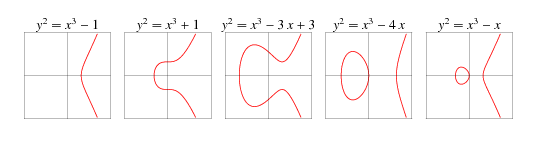
这些曲线具有很好的特性,即在曲线上两点之间绘制的任何非垂直线最多与另一点相交。这使得它们可用于生成非对称密钥对。
0x06 奇怪的对称
仔细看看上面绘制的椭圆曲线。它有几个有趣的特性。
其中之一是水平对称。曲线上的任何点都可以反映在 x 轴上并保持相同的曲线。一个更有趣的特性是任何非垂直线将与曲线相交最多三个位置。
让我们把这条曲线想象成一场奇异的台球比赛。取曲线上的任意两点并在它们之间画一条线,它将与曲线相交的地方恰好是另一处。在这个台球游戏中,你在 A 点拿一个球,将它射向 B 点。当它击中曲线时,球会直接向上弹跳(如果它低于 x 轴)或直接向下弹跳(如果它高于 x -axis) 到曲线的另一侧。
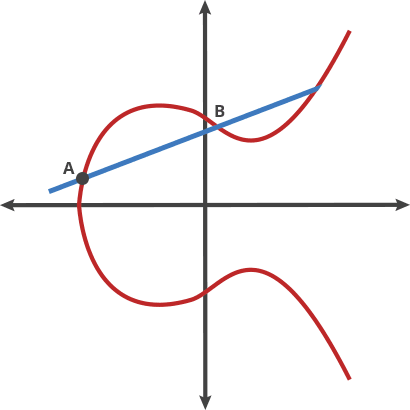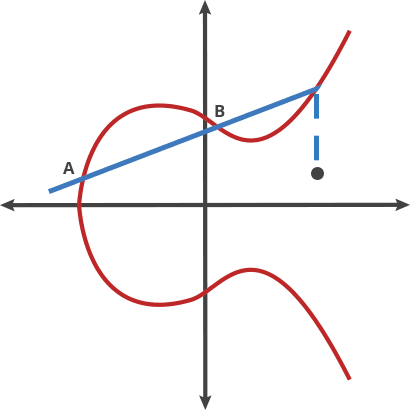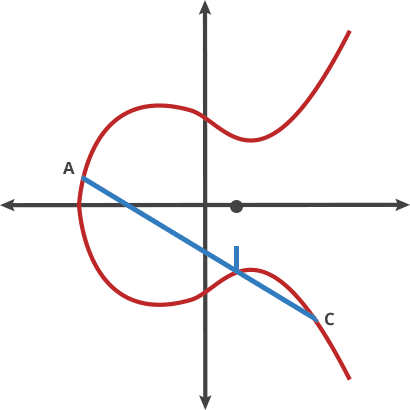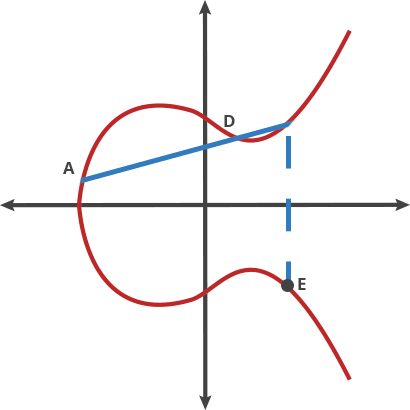
我们可以将这种台球移动称为两点“dot”。曲线上的任意两点都可以点在一起得到一个新点。
A dot B = C
我们还可以将动作串在一起,一遍又一遍地用它自己“dot”一个点。
A dot A = B
A dot B = C
A dot C = D
…
事实证明,如果你有两个点,一个初始点用它自己“点”n次到达一个终点,当你只知道终点而第一个点很难时找出n。继续我们的bizzaro台球比喻,想象一个人在一个房间里独自玩我们的游戏一段时间。按照上述规则,他很容易一遍又一遍地击球。如果有人稍后走进房间并看到球在哪里结束,即使他们知道所有游戏规则以及球从哪里开始,他们也无法确定在没有穿过球的情况下将球击到那里的次数再次整场比赛,直到球到达同一点。易做难撤销:这是一个非常好的陷门功能的基础。
非对称密钥对必须易于生成但难以验证。椭圆曲线密码学的过程是使用两个点来找到从这对产生的唯一的第三个点。使用结果以确定的方式推导出一些相关点。该过程迭代了 n 次以到达最终点。事实证明,如果给你第一个点和最后一个点,在数学上计算 n 是很困难的,n 是你在它们之间必须采取的旅行次数。然而,它很容易验证——正是我们需要的非对称密钥对。
0x07 让我们疯狂吧
上面这条简化曲线非常适合查看和解释椭圆曲线的一般概念,但它并不代表用于密码学的曲线是什么样子。
为此,我们必须将自己限制在固定范围内的数字上,就像在 RSA 中一样。我们不允许曲线上的点有任何值,而是将自己限制为固定范围内的整数。在计算椭圆曲线的公式(y 2 = x 3 + ax + b)时,我们使用相同的技巧,在达到最大值时翻转数字。如果我们选择最大值作为素数,则椭圆曲线称为素数曲线,具有出色的密码学特性。
这是为所有数字绘制的曲线 (y 2 = x 3 – x + 1) 示例:
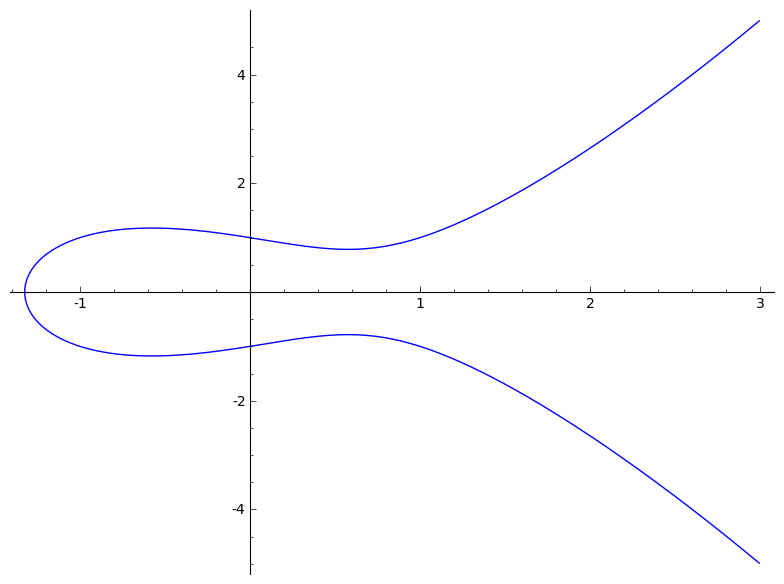
这是同一条曲线的图,仅用最大 97 表示整数点:
这看起来不像传统意义上的曲线,但确实如此。就像原始曲线在边缘被缠绕,只有曲线中到达整数坐标的部分被着色。你甚至可以看到水平对称。

事实上,你仍然可以在这条曲线和圆点上一起玩台球游戏。曲线上的直线方程仍然具有相同的属性。此外,可以有效地计算点运算。您可以将两点之间的线可视化为一条在边界处环绕直到到达一个点的线。就好像在我们奇怪的台球游戏中,当一个球碰到板的边缘(最大值)然后它被神奇地传送到桌子的另一边并继续前进直到到达一个点,有点像游戏小行星.

使用这种新的曲线表示,您可以获取消息并将它们表示为曲线上的点。您可以想象接收一条消息并将其设置为 x 坐标,然后求解 y 以获得曲线上的一个点。在实践中它比这稍微复杂一些,但这是一般的想法。
你得到积分
(70,6), (76,48), -, (82,6), (69,22)
*x 值没有 65 的坐标,这在现实世界中是可以避免的
椭圆曲线密码系统可以通过选择一个素数作为最大值、一个曲线方程和曲线上的一个公共点来定义。私钥是一个数字priv,而公钥是点缀着自身priv时间的公共点。在这种密码系统中从公钥计算出私钥称为椭圆曲线离散对数函数。这就是我们正在寻找的陷门函数。
椭圆曲线离散对数是支撑椭圆曲线密码学的难题。尽管进行了近三年的研究,数学家仍然没有找到一种算法来解决这个问题,改进了幼稚的方法。换句话说,与因式分解不同,根据目前理解的数学,似乎没有捷径可以缩小基于此问题的陷门函数的差距。这意味着对于相同大小的数字,求解椭圆曲线离散对数比分解要困难得多。由于计算量更大的难题意味着更强大的密码系统,因此椭圆曲线密码系统比 RSA 和 Diffie-Hellman 更难破解。
这是椭圆曲线数字签名算法 ECDSA 的核心。根据维基百科,具体步骤概述如下:

与 RSA 相比,ECDSA 数字签名有一个缺点,即它需要良好的熵源。如果没有适当的随机性,私钥可能会被泄露。Wikipedia 继续指出“不仅要求 k 是秘密的,而且为不同的签名选择不同的 k 也是至关重要的,否则步骤 6 中的方程可以求解 d_A,即私钥。这种攻击方法早在 2012 年就已被描述。如果你碰巧重用了k,就很容易解出私钥,直接掏空钱包。
0x08 门限签名
通过(t, n)门限签名,即可将一个秘密(私钥)分成n份,任意 t+1个成员可以通过多轮交互,在不重构私钥的情况下,生成一个有效的签名。
目前主要采用GG18,gg20门限签名方案,其密码生成阶段需要5轮交互,签名阶段需要10轮交互。
0x09 Nonce风险
如果该同一账户签名的交易拥有相同的 RSV 签名的 r 值,签名过程使用了相同的随机数 k。
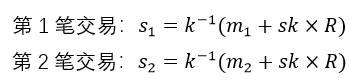

#对于签名: 选择随机数$k$, 计算$R = kG, r = R_x, s = k ^ {-1}(z + rd_A)$, 对于两个采用相同随机数的签名:$(r, s)$ 和 $(r, s')$, 对应的签名消息分别为:$z$ 和 $z'$, 可以得到:
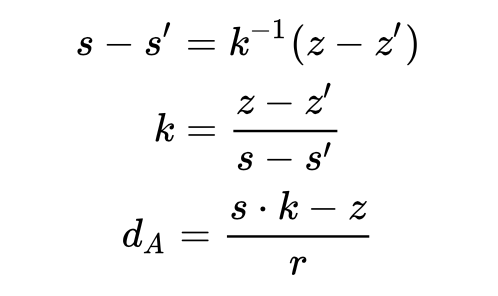
0x10 典型的 MPC
多方安全计算 MPC,Multi-party Computation
在链桥机制中,跨链资产是有锁定账户保管,而锁定账户则是有N个匿名节点经过多方计算(MPC)的方式共同管理。在锁定账户签名过程中,R值是通过N个MPCNode节点通过可验证秘密分享PVSS共同决定,保证不会发生两币交易签名。
具体步骤如下:
1、各Node节点在本地通过真随机数发生器生成一个随机数
2、各Node节点将进行Shamir秘密分享,并将秘密碎片通过安全信道传输给其他节点
3、收到其他节点传输的秘密碎片后,各Node节点在本地进行累加,得到一组秘密碎片,然后将该组秘密碎片与椭圆曲线基点相乘,并将结果广播。
4、各Node节点对广播的数据进行拉格朗日插值计算,得到一个椭圆曲线点,其横坐标即为R值。
首先,R 值是有 N各 节点共同确定的,而不是由单一节点确定,理论上只要 N个 节点中存在 1 个诚实节点,那么 R 值就是随机的;其次,各节点对 R 值贡献的部分是通过真随机数发生器产生的,分布足够均匀。
k 是由 N个Node 节点共同决定,但是由于秘密碎片是通过安全信道传输给各节点,因此没有任何一个节点能够恢复出完整的 k 值。也就是说,k 值是仅仅是一种理论中的存在,能够正常完成 MPC 签名过程,但是确实任何人都不可见的。
0x11 anyswap的解决
1、避免R重复 [https://github.com/anyswap/Anyswap-MPCNode/commit/31f94ff2c8fac19549f6c82b849977730f63bd63]
2、历史的签名会保存在数据库中,新生成的签名随机数判断是否重复[https://github.com/anyswap/CrossChain-Router/commit/ac88cc6861d98645fcdc19d8b985689dd54f5c22]